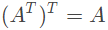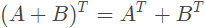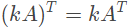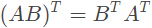矩阵
定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：
矩阵是一个向量组（m个n维向量或n个m维向量）
特殊矩阵
同型矩阵
两个或者两个以上的矩阵的行数和列数都相同，那么我们就说这两个或两个以上的矩阵是同型矩阵。
方阵
行数与列数均为n的矩阵成为n阶方阵。
对称矩阵（Symmetric Matrices）
以主对角线为对称轴，各元素对应相等的方阵。即满足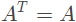
反对称矩阵
即满足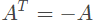
的方阵。对于反对称矩阵，它的主对角线上的元素全为零，而位于主对角线两侧对称的元反号
对角矩阵（diagonal matrix）
主对角线之外的元素皆为0的对称矩阵称为对角矩阵。
数量矩阵（scalar matrix）
对角线上元素相等的对角矩阵称为数量矩阵
单位矩阵（identity matrix）
对角线上元素全为1的对角矩阵称为单位矩阵。
单位矩阵以In表示；如果阶数可忽略，或可由前后文确定的话，也可简记为I。一些数学书籍使用U和E（分别意为单位矩阵和基本矩阵），不过I更加普遍。
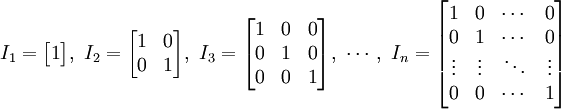
伴随矩阵（adjugate matrix）
定义
设矩阵
，将矩阵
的元素
所在的第i行第j列元素划去后，剩余的各元素按原来的排列顺序组成的n-1阶矩阵所确定的行列式称为元素
的余子式，记为
，称
为元素
的代数余子式。方阵
的各元素的代数余子式
所构成的如下矩阵
=
该矩阵
称为矩阵
的伴随矩阵
逆矩阵（inverse matrix）
一个n阶方阵A称为可逆的，或非奇异（|A|不等于0）的，如果存在一个n阶方阵B，使得AB=BA=E。则称B是A的一个逆矩阵。A的逆矩阵记作A^-1。
性质定理：
可逆矩阵一定是方阵。
如果矩阵A是可逆的，其逆矩阵是唯一的。
A的逆矩阵的逆矩阵还是A。记作（A-1）-1=A。
可逆矩阵A的转置矩阵AT也可逆，并且（AT）-1=（A-1）T(转置的逆等于逆的转置）
(kA)^-1=k^-1·A^-1
|A^-1|=|A|^-1
若矩阵A可逆，则矩阵A满足消去律。即AB=O（或BA=O），则B=O，AB=AC（或BA=CA），则B=C。
两个可逆矩阵的乘积依然可逆。
矩阵可逆当且仅当它是满秩矩阵。
矩阵的秩
存在k阶子式不为0，任给k+1阶子式全为0，则矩阵的秩r(A)=k，即组成矩阵A的独立向量个数为k
矩阵的行列式
定义
设A=(aij)是数域P上的一个n阶方阵，则所有A=(aij)中的元素组成的行列式称为方阵A的行列式，记为|A|或det(A)
性质
- 方阵乘积的行列式等于方阵行列式的乘积，即|AB|=|A|·|B|
- |kA|=k^n|A|
线性运算
加减法
法则
两个矩阵相加减，即它们相同位置的元素相加减
设矩阵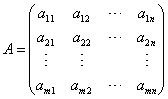
，
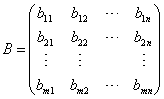，则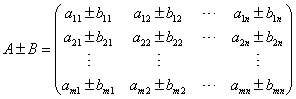
同型矩阵才可进行加减运算
性质
满足交换律：A ± B = B ± A
满足结合律：( A + B ) + C = A + ( B + C )
数乘
法则
数λ乘矩阵A，就是将数λ乘矩阵A中的每一个元素，记为λA或Aλ。特别地，称称为的负矩阵。
性质
满足结合律： (λμ)A=λ(μA) ； (λ+μ)A =λA+μA
满足分配律： λ (A+B)=λA+λB
非线性运算
矩阵转置
定义
将矩阵A的行换成同序号的列所得到的新矩阵称为矩阵A的转置矩阵，记作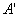
或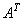
)
性质
矩阵相乘
定义
设A为m×p的矩阵，B为p×n的矩阵，那么称m×n的矩阵C为矩阵A与B的乘积，记作C=AB，其中矩阵C中的第i行第j列元素可以表示为：
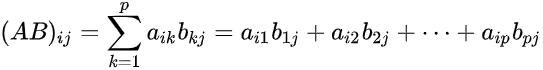
如下所示：
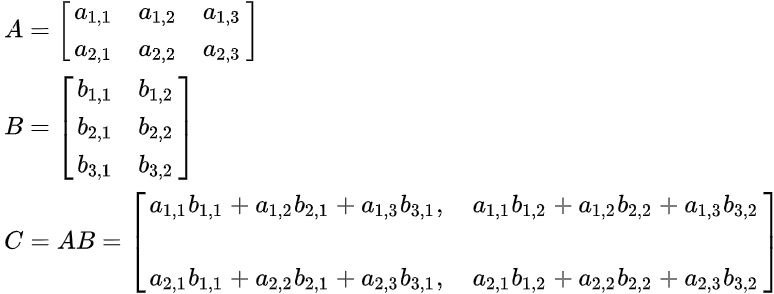
性质
满足结合律： (AB)C=A(BC)
满足左分配律：(A+B)C=AC+BC
满足右分配律：C(A+B)=CA+CB
不满足交换律
